Implied Value in Live $1/$2 No-Limit Hold'em Games

My previous article, "Preflop Raising in Live $1/$2 No-Limit Hold'em Cash Games," I explained how we can estimate what I call the "momentary expected value" (MEV) of our preflop decisions. Conventional poker advice is to make the highest MEV play available. But this is not the full story.
MEV is our expected profit for the hand when it is checked down the rest of the way. This is true because we use showdown equity to calculate our MEV. But we know that few hands actually proceed this way. Generally, our MEV changes once the flop is revealed, usually increasing when we flop well and sometimes decreasing when we whiff.
Furthermore, we have the option of betting when we flop well and check-folding after a whiff. This provides profit leverage on our best flops.
Our hand also has added value when we have position on the villains. For example, when we are heads-up against an easily-read villain, we might win the pot with an inferior hand. However, our position leverage decreases as we face additional villains since it becomes increasingly more difficult to "outplay" additional opponents.
Position is also tremendously valuable when we flop a draw. We have the option of making a strong semi-bluff, often winning the hand outright or reducing the number of villains who stay with us. A flop semi-bluff can also provide us with a free river card, which effectively improves our implied odds for the semi-bluff.
Superior skill can also improve the value of our hand. Of course, our skill is enhanced by our reluctance to play out of position with marginal hands. But our superior skill also improves the profit we make with big hands and decreases our losses when we have a second-best hand.
All of which is to say, having a profitable preflop MEV is a good start, but it is not the only factor in our profit for the completed hand. Our goal should be to make the preflop action that generates the "highest expected value" for the entire hand (HEV), not just the expected value in the moment (MEV).
Consider the curves shown below in Figure 1, which depicts the MEV of limping or raising to $10 on the button in a typical Las Vegas $1/$2 NL cash game when facing 3 limpers. Suppose we have 3?3?, which has MEVRaise = -$0.19 and MEVLimp = -$0.28.
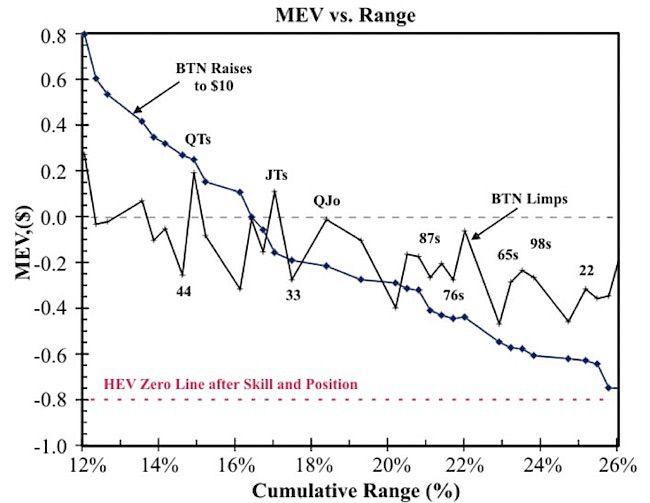
Since both momentary expected values are negative, should we fold our pocket threes on the button? Not usually.
The Value of Skill
Since you are reading this article, you are probably among the most skilled players at your table. So just how much does our superior skill impact our HEV?
Consider the curves in Figure 2, which shows profit versus table position for online NL100 players, based on about 6 million hand histories. The top curve represents the 2,000 players with the highest number of hands dealt to them, while the bottom curve represents the other 119,000 players in the database.
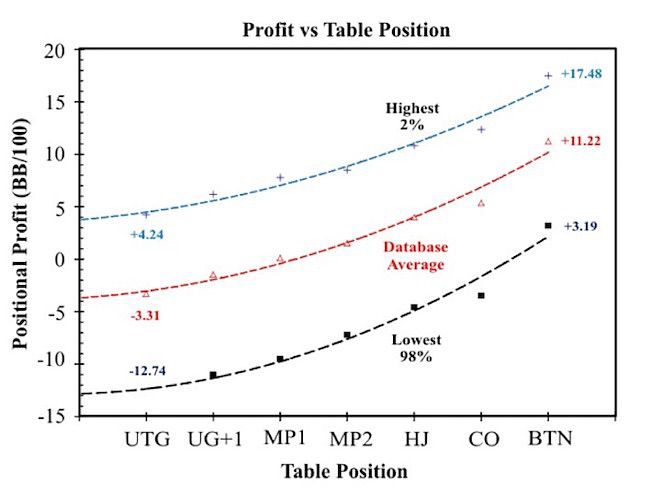
We can see that the most experienced online poker players are much more profitable than the less experienced players, and this is true for every table position. This difference is about 14.3 BB/100 button dealt hands.
But we don't play every button, so we must transform this number into a skill factor for the button hands we do play. Since a skilled player generally plays a lot of hands on the button, the player should be able to perform about 0.3 BB per button-played hands better than the vast majority of opponents in an online game.
Can we transform this online statistic into a skill value for a Vegas $1/$2 game? It's clear from my previous article that the average Vegas $1/$2 player is much worse than the average online player. We also know that the average final pot size is 50 percent larger in the Vegas game for hands which saw a flop after a preflop raise.
On the other hand, Vegas flops contain many more players (on average) than online flops, which makes it more difficult to realize our full skill advantage.
We might reasonably assume that the value of skill in a Vegas $1/$2 game is at least similar to an online NL100 game. We can estimate that our skill value is worth about $0.60 per button. Of course, this is a rough estimate, and will strongly depend on the circumstances of the hand.
Therefore, our Hand EV should be at least HEVRaise = +$0.31 and HEVLimp = $0.22 for our Figure 1 example, considering only our skill advantage. Although our skill advantage might be somewhat less than +$0.60, it should be clear that playing pocket threes on the button should be profitable for us, whether limping or raising.
This is an important result. It implies that we can't play any two cards just because we believe we are superior players. Our arrogance might convince us that the negative-MEV of raising with J?10? against three limpers (-$1.23) can be overcome by our superior skill. It usually cannot. But the negative-MEV of limping with J?10? (-$0.25) might be overcome if our skill advantage is great enough.
The Value of Position
We can also study Figure 2 from the perspective of position.
All three curves indicate that playing under the gun (UTG) is the least profitable position from which to play. This is because we will rarely have superior postflop position. Each subsequent table positon becomes more profitable because we are more and more likely to have superior postflop position. This becomes somewhat complex for the middle position, hijack, and cutoff since we can have superior position over some opponents and inferior position to others.
If we compare the average online profit on the button versus the UTG average, we can see that the button is worth about 13 BB per hundred dealt hands for experienced online players. Since Vegas players are much less positon-aware than are online players, and since Vegas pots are much larger, our positional advantage might be stronger in a Vegas $1/$2 game. On the other hand, Vegas flops contain far more villains, whether limping or raising, which makes it harder to realize our full positional advantage.
We might estimate that the value of the button is about 0.13 BB per dealt-button, or $0.26 per dealt-button in the Vegas game. Considering the large number of hands a good player should play on the button, this might actually be something like $0.50 per button played.
But we can't simply add the value of skill and the value of position together, since the two factors are intertwined. This is because a skilled player is better able to exploit superior position. We can compare the average profit of the skilled players on the button (17.48) with the average profit of the unskilled players under the gun (-12.74) and see that the difference is about 0.3 BB/100 dealt-hands. This is probably a best-case estimate, but it translates to about $0.60 per Vegas dealt button, and perhaps $1.00 per Vegas played button.
So when we combine superior skill with superior position, our enhanced EV is conservatively worth about $0.80 per button in a Vegas $1/$2 game. That means every hand in Figure 1 above the HEV=0 line is playable, though this might vary somewhat depending on the circumstances of the hand.
The Value of Combo Leverage
Combo leverage is the additional value that a starting combo can acquire if it flops well. Suppose again we are on the button with 3?3?, facing 3 limpers. Our MEVRaise = -$0.19 and MEVLimp = -$0.28. So we might expect to lose money by playing this hand if it is always checked down.
But we have a 12 percent chance of flopping a set or better, and we will never check this down. So, we should be able to make a much larger profit when we flop a set than when we whiff the flop. And sometimes the flop will checked around and we will hit our set on the turn, also quite profitable. This is the value of combo leverage.
When we have a starting hand with high implied odds, such as pocket pairs and suited connectors, our Hand EV will be significantly better than our Momentary EV. This means that every pocket pair and suited connector is worth playing on the button in a limped pot in a Vegas $1/$2 game.
We could further modify Figure 1 to adjust "high leverage" combos to a more profitable HEV. We can also construct curves similar to Figure 1 for many other scenarios, including the value of combo leverage, which can provide a general guide for starting hands. These considerations lead to the creation of the "Donkey Poker Starting Hand Chart," which can be found in my book Donkey Poker Volume 1: Preflop.
Conclusion
We can conclude that the EV we calculate preflop (or any other time) should not be our only guide for determining our optimum action. The Momentary EV we calculate preflop for our starting hand must be adjusted, up or down, based on our position, skill, and combo leverage to determine the implied value of our hand.
But the purpose of this article is not to pin down the precise implied value of position, skill, and combo leverage. It is to show that these factors can substantially alter the ranges we can play in low-stakes cash games such as you find in Las Vegas.
Those players who are too tight should consider playing additional hands in late position. Those who are too loose and aggressive should see that they shouldn't play any two cards just because they are confident in their skill. And we should all be able to see that limping is superior to raising for many starting hand combos, contrary to conventional wisdom.
Steve Selbrede has been playing poker for 20 years and writing about it since 2012. He is the author of five books, The Statistics of Poker, Beat the Donks, Donkey Poker Volume 1: Preflop, Donkey Poker Volume 2: Postflop, and Donkey Poker Volume 3: Hand Reading.









